E block homework for Friday

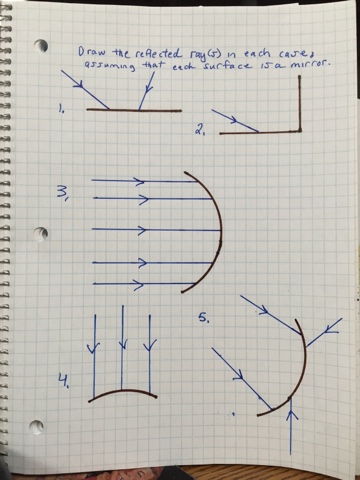
Also, write an accurate statement that describes the law of reflection.  It should stand on its own without pictures, and should be your own description (not swiped from the Internet).

Light 3 - Refraction

Refraction:

Consider a wave hitting a new medium - one in which is travels more slowly. This would be like light going from air into water. The light has a certain frequency (which is unchangeable, since its set by whatever atomic process causes it to be emitted). The wavelength has a certain amount set by the equation, c = f l, where l is the wavelength (Greek symbol, lambda).

When the wave enters the new medium it is slowed - the speed becomes lower, but the frequency is fixed. Therefore, the wavelength becomes smaller (in a more dense medium).

Note also that the wave becomes "bent." Look at the image above: in order for the wave front to stay together, part of the wave front is slowed before the remaining part of it hits the surface. This necessarily results in a bend.

MORE DETAIL:

The general rule - if a wave is going from a lower density medium to one of higher density, the wave is refracted TOWARD the normal (perpendicular to surface) line. See picture above.

Refraction is much different than reflection. In refraction, light enters a NEW medium. In the new medium, the speed changes. We define the extent to which this new medium changes the speed by a simple ratio, the index of refraction:

n = c/v

In this equation, n is the index of refraction (a number always 1 or greater), c is the speed of light (in a vacuum) and v is the speed of light in the new medium.

The index of refraction for some familiar substances:

vacuum, defined as 1

air, approximately 1

water, 1.33

glass, 1.5

polycarbonate ("high index" lenses), 1.67

diamond, 2.2

The index of refraction is a way of expressing how optically dense a medium is. The actual index of refraction (other than in a vacuum) depends on the incoming wavelength. Different wavelengths have slightly different speeds in (non-vacuum) mediums. For example, red slows down by a certain amount, but violet slows down by a slightly lower amount - meaning that red light goes through a material (glass, for example) a bit faster than violet light. Red light exits first.

In addition, different wavelengths of light are "bent" by slightly different amounts. This is trickier to see, but it causes rainbows and prismatic effects.

Some animation, etc.:

http://faraday.physics.utoronto.ca/PVB/Harrison/Flash/Waves/Refraction/Refraction.html

http://www.animations.physics.unsw.edu.au/jw/light/Snells_law_and_refraction.htm

http://www.freezeray.com/flashFiles/Refraction2.htm

https://phet.colorado.edu/en/simulation/bending-light

https://faraday.physics.utoronto.ca/PVB/Harrison/Flash/Optics/Refraction/Refraction.html

And all of this helps explain how lenses form images.

Light 2 - Reflection

Reflection - light "bouncing" off a reflective surface. This obeys a simple law, the law of reflection!

The incident (incoming) angle equals the reflected angle. Angles are generally measured with respect to a "normal" line (line perpendicular to the surface).

Note that this works for curved mirrors as well, though we must think of a the surface as a series of flat surfaces - in this way, we can see that the light can reflect in a different direction, depending on where it hits the surface of the curved mirror.

So - light reflects from mirrors, according to the law of reflection.  However, if the mirrors is curved, light still obeys this rule - it just looks a bit different.  You have to visualize the curved mirror as a series of little flat mirrors.

A convex mirror (top) acts reflects light rays "outward" - the light rays seem as though they are coming from inside the convex mirror, so it seems as though there is an image inside.  We call this a VIRTUAL IMAGE.  Think of convenience store mirrors or side view mirrors.

 A concave mirror (bottom) acts sort of the opposite way.  The parallel light rays bend "inward" - so the light rays converge at a FOCAL POINT.  Where they meet, an image is formed - we call this a REAL IMAGE.

Note however that this happens in this case because the light rays were initially parallel (which is what happens if the object the light rays reflect from is far away).  If they are NOT initially parallel - in other words, if the object is reasonably close to the mirror, the rays may converge at some other point.  Examples of concave mirrors are found in makeup/shaving mirrors and reflecting telescope mirrors.  But again - the light rays ONLY meet at the focal point IF they were initially parallel.  If not, they meet elsewhere (or maybe not at all).  More about this next class when we talk about refraction and lenses.

E block physics

A police car has a frequency that normally makes a 1000 Hz tone.  Calculate the following detected frequencies (f') for these situations:

A.  When you are rest but the police car is moving toward you at 25 m/s.

B.  When the police car is moving toward you at 25 m/s and you are moving away from it at 20 m/s.

C.  When you and the police car are moving toward each other at 30 m/s.

Lux redux!

Recall that waves can be categorized into two major divisions:

Mechanical waves, which require a medium. These include sound, water and waves on a (guitar, etc.) string

Electromagnetic waves, which travel best where there is NO medium (vacuum), though they can typically travel through a medium as well. All electromagnetic waves can be represented on a chart, usually going from low frequency (radio waves) to high frequency (gamma rays). This translates to: long wavelength to short wavelength.

All of these EM waves travel at the same speed in a vacuum: the speed of light (c). Thus, the standard wave velocity equation becomes:

c = f l

where c is the speed of light (3 x 10^8 m/s), f is frequency (in Hz) and l (which should actually be the Greek letter, lambda) is wavelength (in m).

General breakdown of e/m waves from low frequency (and long wavelength) to high frequency (and short wavelength):

Radio

Microwave

IR (infrared)

Visible (ROYGBV)

UV (ultraviolet)

X-rays

Gamma rays

In detail, particularly the last image:

http://hyperphysics.phy-astr.gsu.edu/hbase/ems1.html

http://www.unihedron.com/projects/spectrum/downloads/full_spectrum.jpg

Don't forget - electromagnetic waves should be distinguished from mechanical waves (sound, water, earthquakes, strings on a guitar/piano/etc.). 

ALL E/M waves (in a vacuum) travel at the SPEED OF LIGHT (c).

Doppler!

The Doppler Effect

You have no doubt heard about the Doppler Effect - what is it exactly?  The key in the Doppler effect is that motion makes the "detected" or "perceived" frequencies higher or lower.  We will consider this first for sound and then generalize to light.

Let's play around with this:

http://www.lon-capa.org/~mmp/applist/doppler/d.htm

How how the number of waves you receive per second will be the same regardless of where you stand, UNLESS the source is moving.  And then:

If the source is moving toward you, you detect/measure a higher frequency - this is called a BLUE SHIFT.

If the source is moving away from you, you detect/measure a lower frequency - this is called a RED SHIFT. 

It's worth noting that the effect also works in reverse. If you (the detector) move toward a sound-emitter, you'll detect a higher frequency. If you (the detector) move away from a sound-emitter, you'll detect a lower frequency.

Mind you, these Doppler effects only happen WHILE there is relative motion between source and detector (you).

And they also work for light. In fact, the terms red shift and blue shift refer mainly to light (or other electromagnetic) phenomena.

If your computer runs Java:

http://falstad.com/mathphysics.html

Run the Ripple tank applet -

http://falstad.com/ripple/

Distant galaxies in the universe are moving away from us, as determined by their red shifts. This indicates that the universe is indeed expanding (first shown by E. Hubble). The 2011 Nobel Prize in Physics went to local physicist Adam Riess (and 2 others) for the discovery of the accelerating expansion of the universe. Awesome stuff!

http://www.nobelprize.org/nobel_prizes/physics/laureates/2011/

Test Practice with answers!

1.  How long should an tube (open at both ends) be in order to have a resonant frequency (n=1) of 262 Hz?  (This is C below concert A.)  Assume that the speed of sound is 340 m/s.

2.  How long should a pendulum be so that it swings 3 times per second?

3.  A string is 0.40-m long and has a wave speed of 60 m/s.  Find the wavelengths and frequencies of the first 3 harmonics.

4.  A tube open on both ends is 1.0-m long.  What is the resonant frequency (n=1) of this tube?  Assume that the speed of sound is 340 m/s.  What are the frequencies of the next 2 harmonics?


Answers

1.  0.65 m

2.  f = 3 Hz.  T = 1/3 sec.  L = 0.027 m

3.  0.8 m, 0.4 m, 0.266 m.
     75 Hz, 150 Hz, 225 Hz

4.  170 Hz, 340 Hz, 510 Hz

Notes on tubes/pipes

http://www.acs.psu.edu/drussell/Demos/waves/wavemotion.html

http://www.physicsclassroom.com/class/sound/Lesson-5/Open-End-Air-Columns

http://www.acs.psu.edu/drussell/Demos/rad2/mdq.html

E block fun!

Wave practice!

Work out in your notes.  These will be reviewed on Monday.

Recall also:

v = (frequency)(wavelength)

c = 3 x 10⁸ m/s (speed of light, including any type of electromagnetic wave)

1.  What is the wavelength of the radio station 97.9 ("98 Rock").  Keep in mind that the number refers to the frequency in MHz, and note that MHz means 'million (x 10⁶) Hz."

2.  The visible range of human eyesight is 700 nm to 400 nm.  What are the frequencies associated with this, and which end is red and which is violet?

3.  Find the speed of a 500 Hz wave with a wavelength of 0.4 m.

4.  What is the frequency of a wave that travels at 24 m/s, if 3 full waves fit in a 12-m space?  (Hint:  find the wavelength first.)

5.  Approximately how much greater is the speed of light than the speed of sound?

6.  Harmonics

a.  Draw the first 3 harmonics for a wave on a string.

b.  If the length of the string is 0.5-m, find the wavelengths of these harmonics.

c.  If the frequency of the first harmonic (n = 1) is 15 Hz, find the frequencies of the next 2 harmonics.

d.  Find the speeds of the 3 harmonics.  

7.  (Review) Differentiate between mechanical and electromagnetic waves.  Give examples.

8.  The note C vibrates at 262 Hz (approximately).  Find the frequencies of the next two C’s (1 and 2 octaves above this), and the frequency of the C below it.

9.  A red LED has a wavelength of 662 nm.  What is the frequency of light emitted from it?  (nm refers to x 10^-9 m)

10.  Concert A is defined as 440 Hz.  What are the frequencies of:
a.  A#, which is one semi-tone above A?
b.  C, which is three semi-tones above A?
c.  A-flat, which is one semi-tone below A?

(Recall that a semi-tone is the same as a piano key or guitar fret.)