Circuit constructor (to play with)

https://phet.colorado.edu/en/simulation/circuit-construction-kit-dc

Go to this site, hit download, and then run the program.  Build some practice circuits and use the voltmeter tool (in parallel with any resistor(s) and the ammeter tool (in series) to "measure" currents and voltages.  It's fun - try it!

I have found that this applet is easier to use with a mouse than a trackpad.

HW for E for Wednesday

Use the newly derived formula for Resistors in parallel to hep solve these problems.

1.  What is the total resistance of:

A.  Two 10-ohm resistors in parallel

B.  Three 12-ohm resistors in parallel

(Notice anything convenient about these answers?)

C.  One 4-ohm and one 12-ohm resistor in parallel

2.  A 4-ohm resistor is in series with a 14-ohm resistor.  These are in series with a pair of resistors (3 and 6 ohms) that are in parallel with each other, and a 60-V battery.  Find:

A.  The total resistance of the circuit

B.  All currents and voltages - draw a table to make this a bit easier

E block - for HW Friday / A-block - for HW Monday

Please try the following question:  3 resistors (10, 20, and 30 ohms) are in parallel with a 50-V battery.  Find the following:

- all currents
- all voltages
- total current
- total resistance

Also, try the last problem (combination circuit, #3) on the page handed out in class.  This will be tricky.  See how far you can get with it.

HW for E (Wednesday) and A (Thursday)

Graph I versus R.  Does this graph make sense?  Does it fit an expected mathematical model or equation?

Also, answer these:

Consider a 20-ohm resistor in series with a 12-V battery.  Draw a schematic to represent this and determine the current through the resistor.

Lastly, find definitions and/or pictures of series and parallel circuits.

HW for E and A (Tuesday)

Define the following:

Current

Resistance

HW (for Thursday E and Friday A classes)

Electrostatics homework – to play around with; NOT to be collected

1.  Define charge.

2.  Explain why a charged balloon will stick to a (neutral) wall.

3.  What is the charge (in coulombs) of a electron?

4.  How many protons does it take to make 15 coulomb of charge?

5.  In any atom, which particle(s) are fundamental and which are composite (made of smaller particles)?

6.  You have two clusters of charge:  10 C and 20 C, separated by 1-m of distance.

a.  Use Coulomb’s law to calculate the force that exists between the charges.

b.  Is this force attractive or repulsive?

c.  If you were to quadruple the distance between the charges, what exactly would happen to the amount of force between the charges?

7.  Carbon is element number 6.

a.  What does the 6 represent?

b.  What do you suppose is the difference between Carbon-12 and Carbon-14?

8.  Why do you think that electrons orbit protons (and not the other way around)?

>

Sites from class:

http://www.falstad.com/vector3de/

http://www.falstad.com/emstatic/index.html

Introduction to Electricity

Charge!

Charge

- as fundamental to electricity & magnetism as mass is to mechanics

Charge is a concept used to quantatively related "particles" to other particles, in terms of how they affect each other - do they attract or repel?  If so, with what force?

Charge is represented by letter Q.

The basic idea - likes charges repel (- and -, or + and +) and opposite charges attract (+ and -).

Charge is measured in units called coulombs (C).  A coulomb is a huge amount of charge, but a typical particle has a tiny amount of charge:

- the charge of a proton is 1.6 x 10^-19 C.  Similarly, the charge of an electron is the same number, but negative, by definition (-1.6 x 10^-19 C).  The negative sign distinguishes particles from each other, in terms of whether or not they will attract or repel.  The actual sign is arbitrarily chosen.

The charge of a neutron is 0 C, or neutral.


But what IS charge?

Charge is difficult to define.  It is property of particles that describes how particles interact with other particles. 

In general, the terms are negative and positive, with differing amounts of each, quantified as some multiple of the fundamental charge value (e):

e = 1.6 x 10^-19 C

That's hard to visualize, since a coulomb (c) is a huge amount of charge.  One coulomb, for example, is the charge due to:

1 coulomb = charge due to 6.3 x 10^18 protons

A typical cloud prior to lightning may have a few hundred coulombs of charge - that's an enormous amount of excess charge.

If the charge is negative (-), the excess charge is electrons.

If the charge is positive (+), the excess charge is protons - however, we can NOT easily move protons.  That usually takes a particle accelerator.  Typically, things are charged positively by REMOVING electrons, leaving a net charge of positive.

Other things to remember:

Neutral matter contains an equal number of protons and electrons.

The nucleus of any atom contains protons and (usually) neutrons (which carry no charge).  The number of protons in the nucleus is called the atomic number, and it defines the element (H = 1, He = 2, Li = 3).

Electrons "travel" around the nucleus in "orbitals."  See chemistry for details.  The bulk of the atom is empty space.

Like types of charge repel.  Opposite types of charge attract.

The proton is around 2000 times the mass of the electron and makes up (with the neutrons) the bulk of the atom.  This mass difference also explains why the electron orbits the proton, and not the other way around.

Protons in the nucleus of an atom should, one would imagine, repel each other greatly.  As it happens, the nucleus of an atom is held together by the strong nuclear force (particles which are spring-like, called gluons, keep it together).  This also provides what chemists called binding energy, which can be released in nuclear reactions.

COULOMB'S LAW

How particles interact with each other is governed by a physical relationship called Coulomb's Law:

F = k Q1 Q2 / d^2

Or, the force (of attraction or repulsion) is given by a physical constant times the product of the charges, divided by their distance of separation squared.  The proportionality constant (k) is used to make the units work out to measurable amounts.

Note that this is an inverse square relationship, just like gravity.

The "big 3" particles you've heard of are:

proton
neutron
electron

However, only 1 of these (the electron) is "fundamental".  The others are made of fundamental particles called "quarks""

proton = 2 "up quarks" + 1 "down quark"
neutron = 2 "down quarks" + 1 "up quark"

There are actually 6 types of quarks:  up, down, charm, strange, top, & bottom.  The names mean nothing.

Many particles exist, but few are fundamental - incapable of being broken up further (so far as we know).

In addition, "force-carrying" particles called "bosons" exist -- photons, gluons, W and Z particles.

The Standard Model of Particles and Interactions:

http://www.pha.jhu.edu/~dfehling/particle.gif

practice problem answers

1.

a.  convex (+f)
b.  75 cm
c.  real
d.  -1.5
e.  larger
f.  upside-down
g.  within f

2.

a.  5.2 E 14 Hz
b.  1.7 E 8 m/s
c.  21 degrees
d.  same as a
e.  3.2 E -7 m (or 320 nm)
f.  33.7 degrees

Interference, diffraction, and holography

http://www.falstad.com/ripple/


Interference

Consider 2 waves meeting each other in the same space.  Their energies (amplitudes) can add or subtract.  This phenomenon is called interference.  If you've ever added sine waves on a calculator before, the effect is similar.

Crests can add to other crests, or cancel with troughs.  However, it is usually some combination (depending on the waves in question).  And often, beautiful "interference patterns" can result.

Diffraction is the phenomenon wherein light waves pass through small openings - the openings cause "new" waves to form, and these "new" waves interfere with each other.

Diffraction and Holography

Holography

Holography is a direct application of interference patterns - indeed, it is the recording of an interference pattern on film, reconstructed with a laser.

Holography is an interference phenomenon caused by two beams - a reference beam (coming from a laser), and an object beam (which reflects off the object).  This interference pattern is burned into the film emulsion of the holographic film.  It can be reconstructed when light passes through it again.

Test practice

1.  Consider a lens with a +30 cm focal length.  An object is 50 cm from the center of lens.  Find the following:

a.  type of lens
b.  location of image (di)
c.  type of image (real/virtual)
d.  magnification of image
e.  whether image is larger or smaller than original object
f.  whether image is upside-down or rightside-up
g.  where should you place the object so that you ONLY get virtual images

2.  Review from the older optics stuff:

Consider a rectangular plastic box (n = 1.8).  Light of wavelength 575 nm is sent into the block at a 40-degree angle (with respect to a normal line).  Find the following:

a.  frequency of light outside box
b.  speed of light inside box
c.  angle of light inside box
d.  frequency of light inside box
e.  wavelength of light inside box
f.  critical angle of this plastic

Upcoming deadlines

E block:

5/8 (Monday):  lab draft due

5/10 (Wednesday):  Optics test

5/12 (Friday):  Final lab due


A block:

5/9 (Tuesday):  lab draft due\

5/11 (Thursday):  Optics test

5/15 (Monday):  Final lab due

Lens simulations

https://phet.colorado.edu/sims/geometric-optics/geometric-optics_en.html

https://graphics.stanford.edu/courses/cs178-10/applets/thinlens.html

http://www.physicsclassroom.com/Physics-Interactives/Refraction-and-Lenses/Optics-Bench/Optics-Bench-Refraction-Interactive

https://simbucket.com/lensesandmirrors/

Deriving the Lens Equation

Lab questions

These are the same ones that were already in the lab handout - nothing new here.

1)      Mathematically, what is the distinction between real and virtual images?

2)      Mathematically, what is the distinction between convex and concave lenses?

3)      Are there any object distances (d_o) where NO images should appear?

4)      What exactly is f, the focal point/length?  What factor(s) do you suppose determines the f of a lens?

5)      What is the effect of covering half of the lens?  Does it matter how you cover it?

6)      What happens to the image formed as the object distance nears the focal point (f)?  Mathematically, what is happening?

7)      Mathematically, how can we predict whether or not an image is larger or smaller, right-side up or upside-down?

8)      How are lenses and mirrors similar and different?

Formal lab guidelines (same as what was emailed to you); Questions are forthcoming.

Formal Group Lab - Optics

 (largely lifted and slightly modified from Wagner, T. and R. Sanford. 2005. Environmental Science: Active learning laboratories and applied problem sets. John Wiley & Sons, Hoboken, NJ; special thanks to Jeff Jennings.)

This formal lab write-up will follow the explicit format that most scientific papers follow.  Scientific papers are not literary works - instead, they are meant to transmit information effectively and concisely.  There’s no option, for example, for surprise endings in scientific papers—the answer is always given in the first section.  

Your group’s paper will be broken down into the following sections.  Every section, except the title, should be labeled.  

Laboratory reports are your tool for expressing what you did, why you did it, and what you learned in the process.  Even if your understanding of the procedure, techniques, and results is perfect and your results are error-free, a poorly written report will suggest that you did not understand what you have done.  Writing reports is not difficult if you remember a few guidelines about writing and the structure of a good report.  An excellent resource to help you prepare, organize, interpret, and write you formal laboratory report is Labwrite.  Labwrite is an instructional project originating from North Carolina State University and sponsored by the National Science Foundation.  The Labwrite site is: http://labwrite.ncsu.edu

Your formal lab report must have the following components in the following order.

• Title
• Abstract
• Introduction
• Materials and Methods
• Results
• Discussion
• Literature Cited (or References)

Note:  Metric measurements are used in science for presenting facts and figures.  When presenting information to the general public (i.e. not in a formal lab reports or scientific conference), English units are often used.

Title   

“What did you study?” 

The title of a lab report should indicate exactly what you studied.  The title should give the reader a concise, informative description of the content and scope of the paper.  For example, not “Wave Lab” but rather “An investigation into harmonics on a string.”

Abstract  

“Summarize, please.”

This is a concise summary of the major findings of the study. It is generally no longer than 9–10 sentences, or half a page.  It should state the purposes of the study, briefly summarize the methods, major results, and major conclusions of the study. The abstract should stand alone: do not refer to any figures or tables, or cite any references.  Generally scientists write the abstract last, because you need to know exactly what is in the paper before you can summarize it.

Introduction        

“Why did you study this phenomenon?”  And don’t just say, “Because Sean told us to.”

This is where you give a brief background to your experiment.  It usually includes background information, including the work of others, and a description of your objectives.  Normally, you would state the specific hypothesis/predictions you will be testing and give theoretical justifications for them.  In this optics lab, however, I did not give you any choice before the lab – change your writing accordingly.  Since I did not ask you to generate a hypothesis, so there is no need to include one.

Note:  You may want to refer to other work in the field (be sure to cite your sources!).  Direct quotes are rarely used in scientific writing; instead state the findings of others in your own words. We will not be using footnotes but rather be citing the author by last name, and the year that the source was published (Lally, 2008).  At the end of the paper you will then need to have the complete bibliographic listing for the reference.  See reference section for further explanation.

 

Materials and Methods  

      

“What did you do?  How did you do it?”

This section is a very concise summary of the subjects, equipment, and procedures used.  This section should contain enough information so that someone else could duplicate your experiment. It is not a list, but a narrative description.  However be careful that you don’t go over board and include superfluous information that is not relevant, such as, “then go over and pick up the following supplies…”  If you are following the methods of another paper or a lab manual, cite the source.  Also remember that these are not cooking directions but should be in the passive past tense as in, “We filled six petri dishes with 20 ml of tap water in each.”  It is also critical to include all relevant details such as lengths, number of trials, time intervals…etc.  A common mistake is to let results creep into this section.

Results         

“What did you find?”

In the results section, you present your observations and data with no interpretations or conclusions about what they mean; that is for the discussion.  Tables and figures should be used to supplement the text and to present the data in a synthesized, more understandable form.  Use the past tense to describe your results.  Think of this section as a simple description of your major results.  This is also where you include relevant sample calculations (such as experimental focal length) with your data (and related statistics such as percent error).

Do not present your raw data.  Instead, present data in an easy to read form.  You will probably use a figure or a table to present your results.  All tables and figures must be numbered and have self-explanatory titles so that the reader can understand their content without the text (e.g. Table 1.  Displacement of falling ball versus time).  Assign numbers to tables and figures in the order they are mentioned in the text.  Tables and figures are numbered independently of each other (i.e. Table 1 and 2, and then Figure 1 and 2).  Tables are labeled at the top and figures at the bottom.  Tables are referred to as tables; all other items (graphs, photographs, drawings, diagrams, maps, etc.) are referred to as figures.

Discussion    

    

“What does it mean?”

This is the meat of your paper.  Here you are to give a reader the “take home” message of the study.  This section should respond to and echo concepts brought up in the introduction without being repetitive.  Begin by briefly summarizing the major findings of your study. Then discuss each finding one at a time (usually in separate paragraphs).  The support you provide for your ideas is very important.  Use your data, trends, statistical evidence and background information as support.  Remember that you rarely if ever “prove” something, but that your data can be used in support of a particular conclusion.  Do not make statements that cannot be supported by the data.  Discuss possible errors (threats to validity) in the experiment, but don’t make the common mistake that beginning writers often do, of focusing completely on potential errors in your work.  Not all potential errors may be significant.

Questions to consider

In this lab, I want you and your group to consider a few “extension questions” – things that are not obvious and may indeed be hard to prove.  These questions will be posted on the blog shortly.

Concluding remarks

Anything else worth remarking about that does not neatly fit into the “Discussion” section.

Acknowledgements

This is where you would typically thank those who funded a study or anyone whose expertise you found helpful.

References or Literature Cited

Sources must be credited if you obtain ideas or thoughts from them, even if you are not giving a direct quote.  There are a number of different formats used in science for citation.  Use the format below to cite any literature used in your report (e.g. a textbook, journal articles, books, internet and so forth).  In the text of your report cite references using the author’s surnames, and the year of publication in parenthesis (e.g. Botkin and Keller, 2003).  These sources then have full bibliographic listings in this section of the paper. 

Journal articles

Single Author

Connell, J.L. 1974. Species Diversity in Tropical Coral Reefs. Science 234:23-26.

Multiple Authors

O’Rourke, D., L. Connelly, and C.P. Koshland. 1996. Industrial Ecology: A Critical Review. International Journal of Environmental Pollution 6:89-112.

Books
Single Author

Forsyth, A. 2001. A Natural History of Sex: The ecology and evolution of mating behavior. Firefly Books, Buffalo, NY.

Multiple Authors

Starr, C., C.A. Evers and L. Starr. 2008. Biology. 7^th ed. Thomson Brooks/Cole, CA

Chapter in a Book

Rabe, G.B. 1999. Sustainability in a Regional Context: The case of the Great Lakes basin. P. 248-281. In D.A. Mazmanian and M.E. Kraft (ed.) Towards Sustainable Communities: Transition and transformations in environmental policy. MIT Press, Cambridge, MA.

Internet

Citations for internet sites should be similar to print media citations, including author, publication date, article title, site title, URL, and date the information was posted (or when the address was accessed).

Internet article

Sanchirico, J.N. and R.G. Newell. 2003. Carching Market Efficicienceds: Quota-based fisheries management. Resources 150 [Online], 23 Sept. 2003. Available at http://www.rff.org/rff/documents/rff-resources-150-carchmarket.pdf. (verified 2 June 2004)

Web page (with no author listed)
Emerald Ash Borer (EAB) [Internet]. [updated 2007 Feb 27]. Columbus (OH): Ohio Department of Natural Resources, Division of Forestry; [cited 2007 Jul 24]. Available from: http://www.dnr.state.oh.us/forestry/health/eab.htm

In-Text:
(Emerald Ash Borer ... [updated 2007])

Government Website

U.S. Environmental Protection Agency (US EPA). 2004. Home Page [Online]. Available at http://www.epa.gov (verified 3 June 2004)

Laboratory Write-ups Check List

 

Title

• Title stated clearly and concisely.
• Includes the correct independent and dependent variables
• Title capitalized
• Names, in alphabetical order (assuming that there is no “lead author”)

Abstract

• Clear, succinct explanation of question being addressed
• Clear, succinct explain of research
• Includes conclusions of research
• Under 10 sentences

Introduction

• Introduction to conceptual framework of research
• Starts with broad background material and narrows to introduce this particular research
• Clear description of question being addressed

Material and Methods

• Protocol is written in essay form (not numbered steps) in past passive tense (“a transect was placed …”)
• Protocol clearly establishes proper set of procedures that would allow it to be replicated
• Superfluous steps NOT included

Results

• All figures and tables have appropriately descriptive legends
• Metric units used
• All figures have appropriate labels on axes and tables have appropriate column headings
• Figures and tables used to support written explanation of results
• Explicit use of data used in text

Discussion

• Analysis of results using explicit data and referencing figures and tables
• Proper use of references to information obtained from other sources
• Attempt to describe and explain trends and anomalies seen in data.

Questions

Concluding remarks

Acknowledgements

References

• Accurate and clear

HW for E (for Monday) and A (Tuesday)

Hiya.

Perform some calculations related to your lab.  Behold - the thin lens equation (also known as the lens/mirror equation):

Use this equation to solve for f for each case where you have do and di data.  You have a theoretical f (10 or 20 cm, given by the manufacturer of the lens or mirror you used).  You are going to determine an experimental version - essentially, comparing your work to their claim.

It is probably easiest to solve the above equation algebraically first - solving for f.  To wit:

f = (do di) /  (do + di)

Determine the experimental values of f for all of your trials.  All lab group members should do this before the next class.

Next, determine percent errors of your value from the claimed f:

% error = [ (exp f - theo f) / (theo f) ] * 100

The easiest path for all of this is to use a spreadsheet to do the calculations.

HW for Thursday (E) and Friday (A)

Please look up the following and be able to distinguish between the two:

Real image
Virtual image

Also, read the lab handout, please.  A block - you'll get the lab handout Wednesday before the quiz.

Thanks everyone!

Quiz practice

Consider a 650 nm laser beam.  It heads into a block of plastic (n = 1.7) at an initial angle of 40 degrees.  Find the following:

a.  angle of refraction

b.  frequency inside the block

c.  wavelength inside the block

d.  critical angle of the block

e.  speed of light inside the block

Be sure to review how to draw "normal lines" (perpendicular) and predict the path that light takes upon entering a new medium.

Snell's law derived

E and A block homework

Please come to class with definitions of:

- Index of refraction
- Snell's law - with an equation, if possible, with a diagram and/or variables explained

E block homework for Friday

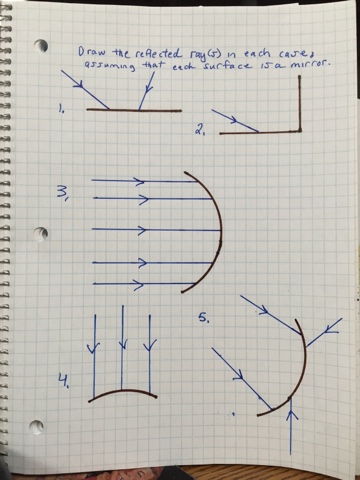
Also, write an accurate statement that describes the law of reflection.  It should stand on its own without pictures, and should be your own description (not swiped from the Internet).

Light 3 - Refraction

Refraction:

Consider a wave hitting a new medium - one in which is travels more slowly. This would be like light going from air into water. The light has a certain frequency (which is unchangeable, since its set by whatever atomic process causes it to be emitted). The wavelength has a certain amount set by the equation, c = f l, where l is the wavelength (Greek symbol, lambda).

When the wave enters the new medium it is slowed - the speed becomes lower, but the frequency is fixed. Therefore, the wavelength becomes smaller (in a more dense medium).

Note also that the wave becomes "bent." Look at the image above: in order for the wave front to stay together, part of the wave front is slowed before the remaining part of it hits the surface. This necessarily results in a bend.

MORE DETAIL:

The general rule - if a wave is going from a lower density medium to one of higher density, the wave is refracted TOWARD the normal (perpendicular to surface) line. See picture above.

Refraction is much different than reflection. In refraction, light enters a NEW medium. In the new medium, the speed changes. We define the extent to which this new medium changes the speed by a simple ratio, the index of refraction:

n = c/v

In this equation, n is the index of refraction (a number always 1 or greater), c is the speed of light (in a vacuum) and v is the speed of light in the new medium.

The index of refraction for some familiar substances:

vacuum, defined as 1

air, approximately 1

water, 1.33

glass, 1.5

polycarbonate ("high index" lenses), 1.67

diamond, 2.2

The index of refraction is a way of expressing how optically dense a medium is. The actual index of refraction (other than in a vacuum) depends on the incoming wavelength. Different wavelengths have slightly different speeds in (non-vacuum) mediums. For example, red slows down by a certain amount, but violet slows down by a slightly lower amount - meaning that red light goes through a material (glass, for example) a bit faster than violet light. Red light exits first.

In addition, different wavelengths of light are "bent" by slightly different amounts. This is trickier to see, but it causes rainbows and prismatic effects.

Some animation, etc.:

http://faraday.physics.utoronto.ca/PVB/Harrison/Flash/Waves/Refraction/Refraction.html

http://www.animations.physics.unsw.edu.au/jw/light/Snells_law_and_refraction.htm

http://www.freezeray.com/flashFiles/Refraction2.htm

https://phet.colorado.edu/en/simulation/bending-light

https://faraday.physics.utoronto.ca/PVB/Harrison/Flash/Optics/Refraction/Refraction.html

And all of this helps explain how lenses form images.

Light 2 - Reflection

Reflection - light "bouncing" off a reflective surface. This obeys a simple law, the law of reflection!

The incident (incoming) angle equals the reflected angle. Angles are generally measured with respect to a "normal" line (line perpendicular to the surface).

Note that this works for curved mirrors as well, though we must think of a the surface as a series of flat surfaces - in this way, we can see that the light can reflect in a different direction, depending on where it hits the surface of the curved mirror.

So - light reflects from mirrors, according to the law of reflection.  However, if the mirrors is curved, light still obeys this rule - it just looks a bit different.  You have to visualize the curved mirror as a series of little flat mirrors.

A convex mirror (top) acts reflects light rays "outward" - the light rays seem as though they are coming from inside the convex mirror, so it seems as though there is an image inside.  We call this a VIRTUAL IMAGE.  Think of convenience store mirrors or side view mirrors.

 A concave mirror (bottom) acts sort of the opposite way.  The parallel light rays bend "inward" - so the light rays converge at a FOCAL POINT.  Where they meet, an image is formed - we call this a REAL IMAGE.

Note however that this happens in this case because the light rays were initially parallel (which is what happens if the object the light rays reflect from is far away).  If they are NOT initially parallel - in other words, if the object is reasonably close to the mirror, the rays may converge at some other point.  Examples of concave mirrors are found in makeup/shaving mirrors and reflecting telescope mirrors.  But again - the light rays ONLY meet at the focal point IF they were initially parallel.  If not, they meet elsewhere (or maybe not at all).  More about this next class when we talk about refraction and lenses.

E block physics

A police car has a frequency that normally makes a 1000 Hz tone.  Calculate the following detected frequencies (f') for these situations:

A.  When you are rest but the police car is moving toward you at 25 m/s.

B.  When the police car is moving toward you at 25 m/s and you are moving away from it at 20 m/s.

C.  When you and the police car are moving toward each other at 30 m/s.

Lux redux!

Recall that waves can be categorized into two major divisions:

Mechanical waves, which require a medium. These include sound, water and waves on a (guitar, etc.) string

Electromagnetic waves, which travel best where there is NO medium (vacuum), though they can typically travel through a medium as well. All electromagnetic waves can be represented on a chart, usually going from low frequency (radio waves) to high frequency (gamma rays). This translates to: long wavelength to short wavelength.

All of these EM waves travel at the same speed in a vacuum: the speed of light (c). Thus, the standard wave velocity equation becomes:

c = f l

where c is the speed of light (3 x 10^8 m/s), f is frequency (in Hz) and l (which should actually be the Greek letter, lambda) is wavelength (in m).

General breakdown of e/m waves from low frequency (and long wavelength) to high frequency (and short wavelength):

Radio

Microwave

IR (infrared)

Visible (ROYGBV)

UV (ultraviolet)

X-rays

Gamma rays

In detail, particularly the last image:

http://hyperphysics.phy-astr.gsu.edu/hbase/ems1.html

http://www.unihedron.com/projects/spectrum/downloads/full_spectrum.jpg

Don't forget - electromagnetic waves should be distinguished from mechanical waves (sound, water, earthquakes, strings on a guitar/piano/etc.). 

ALL E/M waves (in a vacuum) travel at the SPEED OF LIGHT (c).

Doppler!

The Doppler Effect

You have no doubt heard about the Doppler Effect - what is it exactly?  The key in the Doppler effect is that motion makes the "detected" or "perceived" frequencies higher or lower.  We will consider this first for sound and then generalize to light.

Let's play around with this:

http://www.lon-capa.org/~mmp/applist/doppler/d.htm

How how the number of waves you receive per second will be the same regardless of where you stand, UNLESS the source is moving.  And then:

If the source is moving toward you, you detect/measure a higher frequency - this is called a BLUE SHIFT.

If the source is moving away from you, you detect/measure a lower frequency - this is called a RED SHIFT. 

It's worth noting that the effect also works in reverse. If you (the detector) move toward a sound-emitter, you'll detect a higher frequency. If you (the detector) move away from a sound-emitter, you'll detect a lower frequency.

Mind you, these Doppler effects only happen WHILE there is relative motion between source and detector (you).

And they also work for light. In fact, the terms red shift and blue shift refer mainly to light (or other electromagnetic) phenomena.

If your computer runs Java:

http://falstad.com/mathphysics.html

Run the Ripple tank applet -

http://falstad.com/ripple/

Distant galaxies in the universe are moving away from us, as determined by their red shifts. This indicates that the universe is indeed expanding (first shown by E. Hubble). The 2011 Nobel Prize in Physics went to local physicist Adam Riess (and 2 others) for the discovery of the accelerating expansion of the universe. Awesome stuff!

http://www.nobelprize.org/nobel_prizes/physics/laureates/2011/

Test Practice with answers!

1.  How long should an tube (open at both ends) be in order to have a resonant frequency (n=1) of 262 Hz?  (This is C below concert A.)  Assume that the speed of sound is 340 m/s.

2.  How long should a pendulum be so that it swings 3 times per second?

3.  A string is 0.40-m long and has a wave speed of 60 m/s.  Find the wavelengths and frequencies of the first 3 harmonics.

4.  A tube open on both ends is 1.0-m long.  What is the resonant frequency (n=1) of this tube?  Assume that the speed of sound is 340 m/s.  What are the frequencies of the next 2 harmonics?


Answers

1.  0.65 m

2.  f = 3 Hz.  T = 1/3 sec.  L = 0.027 m

3.  0.8 m, 0.4 m, 0.266 m.
     75 Hz, 150 Hz, 225 Hz

4.  170 Hz, 340 Hz, 510 Hz

Notes on tubes/pipes

http://www.acs.psu.edu/drussell/Demos/waves/wavemotion.html

http://www.physicsclassroom.com/class/sound/Lesson-5/Open-End-Air-Columns

http://www.acs.psu.edu/drussell/Demos/rad2/mdq.html

E block fun!

Wave practice!

Work out in your notes.  These will be reviewed on Monday.

Recall also:

v = (frequency)(wavelength)

c = 3 x 10⁸ m/s (speed of light, including any type of electromagnetic wave)

1.  What is the wavelength of the radio station 97.9 ("98 Rock").  Keep in mind that the number refers to the frequency in MHz, and note that MHz means 'million (x 10⁶) Hz."

2.  The visible range of human eyesight is 700 nm to 400 nm.  What are the frequencies associated with this, and which end is red and which is violet?

3.  Find the speed of a 500 Hz wave with a wavelength of 0.4 m.

4.  What is the frequency of a wave that travels at 24 m/s, if 3 full waves fit in a 12-m space?  (Hint:  find the wavelength first.)

5.  Approximately how much greater is the speed of light than the speed of sound?

6.  Harmonics

a.  Draw the first 3 harmonics for a wave on a string.

b.  If the length of the string is 0.5-m, find the wavelengths of these harmonics.

c.  If the frequency of the first harmonic (n = 1) is 15 Hz, find the frequencies of the next 2 harmonics.

d.  Find the speeds of the 3 harmonics.  

7.  (Review) Differentiate between mechanical and electromagnetic waves.  Give examples.

8.  The note C vibrates at 262 Hz (approximately).  Find the frequencies of the next two C’s (1 and 2 octaves above this), and the frequency of the C below it.

9.  A red LED has a wavelength of 662 nm.  What is the frequency of light emitted from it?  (nm refers to x 10^-9 m)

10.  Concert A is defined as 440 Hz.  What are the frequencies of:
a.  A#, which is one semi-tone above A?
b.  C, which is three semi-tones above A?
c.  A-flat, which is one semi-tone below A?

(Recall that a semi-tone is the same as a piano key or guitar fret.)

Notes on music FYI

Music 1 - Notes and Harmonics

In western music, we use an "equal tempered (or well tempered) scale."  It has a few noteworthy characteristics;

The octave is defined as a doubling (or halving) of a frequency.

You may have seen a keyboard before.  The notes are, beginning with C (the note immediately before the pair of black keys):

C

C#

D

D#

E

F

F#

G

G#

A

A#

B

C

(Yes, I could also say D-flat instead of C#, but I don't have a flat symbol on the keyboard.  And I don't want to split hairs over sharps and flats - it's not that important at the moment.)

There are 13 notes here, but only 12 "jumps" to go from C to the next C above it (one octave higher).  Here's the problem.  If there are 12 jumps to get to a factor of 2 (in frequency), making an octave, how do you get from one note to the next note on the piano?  (This is called a "half-step" or "semi-tone".)

The well-tempered scale says that each note has a frequency equal to a particular number multiplied by the frequency that comes before it.  In other words, to go from C to C#, multiply the frequency of the C by a particular number.

So, what is this number?  Well, it's the number that, when multiplied by itself 12 times, will give 2.  In other words, it's the 12th root of 2 - or 2 to the 1/12 power.  That is around 1.0594.

So to go from one note to the next note on the piano or fretboard, multiply the first note by 1.0594.  To go TWO semi-tones up, multiply by 1.0594 again - or multiply the first note by 1.0594^2.  Got it?

>

Recalling harmonics

Let us recall "harmonics", visible on a string (as demonstrated in the recent lab).  Harmonics are wave shapes produced that have a maximum amplitude under given conditions (tension in string, length of string, composition of string, etc.).  Every stretched string has a particular lowest frequency at which it will naturally resonate or vibrate.  However, there are also higher frequencies that will also give "harmonics" - basically, pretty wave shapes (also known as "standing waves").  These higher frequencies are integer multiples of the lowest frequency.

So, if the frequency of the lowest frequency is 10 Hz (for an n = 1 harmonic), the next harmonic (n = 2) occurs at 20 Hz.  N = 3 is at 30 Hz, and so on.

For those of you who play guitar, you know that you get harmonics by lightly touching the strings at certain locations.  In the exact center of the neck (12th fret) you get a harmonic (the 2nd one) and the frequency is twice that of the open string - one octave above, as we will discuss.

A block problems to work on IN CLASS Tuesday

Wave practice!

Work out in your notes.  These will be reviewed on Thursday.

Recall also:

v = (frequency)(wavelength)

c = 3 x 10⁸ m/s (speed of light, including any type of electromagnetic wave)

1.  What is the wavelength of the radio station 97.9 ("98 Rock").  Keep in mind that the number refers to the frequency in MHz, and note that MHz means 'million (x 10⁶) Hz."

2.  The visible range of human eyesight is 700 nm to 400 nm.  What are the frequencies associated with this, and which end is red and which is violet?

3.  Find the speed of a 500 Hz wave with a wavelength of 0.4 m.

4.  What is the frequency of a wave that travels at 24 m/s, if 3 full waves fit in a 12-m space?  (Hint:  find the wavelength first.)

5.  Approximately how much greater is the speed of light than the speed of sound?

6.  Harmonics

a.  Draw the first 3 harmonics for a wave on a string.

b.  If the length of the string is 0.5-m, find the wavelengths of these harmonics.

c.  If the frequency of the first harmonic (n = 1) is 15 Hz, find the frequencies of the next 2 harmonics.

d.  Find the speeds of the 3 harmonics.  

7.  (Review) Differentiate between mechanical and electromagnetic waves.  Give examples.

8.  The note C vibrates at 262 Hz (approximately).  Find the frequencies of the next two C’s (1 and 2 octaves above this), and the frequency of the C below it.

9.  A red LED has a wavelength of 662 nm.  What is the frequency of light emitted from it?  (nm refers to x 10^-9 m)

10.  Concert A is defined as 440 Hz.  What are the frequencies of:
a.  A#, which is one semi-tone above A?
b.  C, which is three semi-tones above A?
c.  A-flat, which is one semi-tone below A?

(Recall that a semi-tone is the same as a piano key or guitar fret.)

More quiz practice - answers at bottom

Hey everyone,

By popular request, here are a few more quiz practice problems.

1.  How long should a pendulum be so that it has a 1.5 second period?  Also, what is the frequency of oscillation of this pendulum?

2.  Consider a 0.5-kg box sliding down a frictionless incline.  If it drops a total of 0.75 during the descent, find the following:

a.  initial PE relative to the bottom of the slide
b.  KE at the bottom of the slide
c.  speed at the bottom of the slide
d.  speed half-way down the slide

3.  A Telecaster guitar string is approximately 0.64-m long from bridge to "nut" (where the strings connect to the headstock).  Perform calculations for the first 3 harmonics, assuming that the lowest frequency (n=1) is 320 Hz.  Fill in the table below:

n          harmonic drawing          wavelength          frequency          speed

1                                                                                 320

2

3


>

Answers:

1.  0.56 m

2.

3.7 J
3.7 J
3.8 m/s
2.7 m/s

3.  with rounding, answers will be close to these:

1     1.28 m     320 Hz     410 m/s
2     0.64 m     640 Hz     410 m/s
3     0.43 m     960 Hz     410 m/s

Wave stuff

So - Waves.....  

We spoke about energy.  Energy can, as it turns out, travel in waves.  In fact, you can think of a wave as a traveling disturbance, capable of carrying energy with it.  For example, light "waves" can have energy - like solar energy.  Ocean waves can certainly carry energy.  

There are several wave characteristics (applicable to most conventional waves) that are useful to know:

amplitude - the "height" of the wave, from equilibrium (or direction axis of travel) to maximum position above or below

crest - peak (or highest point) of a wave

trough - valley (or lowest point) of a wave

wavelength (lambda - see picture 2 above) - the length of a complete wave, measured from crest to crest or trough to trough (or distance between any two points that are in phase - see picture 2 above).  Measured in meters (or any units of length).

frequency (f) - literally, the number of complete waves per second.  The unit is the cycle per second, usually called:  hertz (Hz)

wave speed (v) -  the rate at which the wave travels.  Same as regular speed/velocity, and measured in units of m/s (or any unit of velocity).  It can be calculated using a simple expression:

There are 2 primary categories of waves:

Mechanical – these require a medium (e.g., sound, guitar strings, water, etc.)

Electromagnetic – these do NOT require a medium and, in fact, travel fastest where is there is nothing in the way (a vacuum). All e/m waves travel at the same speed in a vacuum (c, the speed of light):

c = 3 x 10^8 m/s

First, the electromagnetic (e/m) waves:

General breakdown of e/m waves from low frequency (and long wavelength) to high frequency (and short wavelength):

Radio

Microwave

IR (infrared)

Visible (ROYGBV)

UV (ultraviolet)

X-rays

Gamma rays

In detail, particularly the last image:

http://hyperphysics.phy-astr.gsu.edu/hbase/ems1.html

http://csep10.phys.utk.edu/astr162/lect/light/spectrum.html

http://www.unihedron.com/projects/spectrum/downloads/full_spectrum.jpg

Mechanical waves include:  sound, water, earthquakes, strings (guitar, piano, etc.)....

Again, don't forget that the primary wave variables are related by the expression:

v = f l

speed = frequency x wavelength

(Note that 'l' should be the Greek symbol 'lambda', if it does not already show up as such.)

For e/m waves, the speed is the speed of light, so the expression becomes:

c = f l

Note that for a given medium (constant speed), as the frequency increases, the wavelength decreases.